Latent Factor 모형 (PCA와 Latent Factor 모형)

5. Latent Factor 모형 (PCA와 Latent Factor 모형)¶

• Latent Factor 모형은 복잡한 사용자/영화 특성을 몇 개의 벡터로 간략화해보겠다는 모형
• 평점을 사용자 요인 행렬, 별점 요인 행렬의 곱으로 이루어진 행렬로 보고, SVD등과 같은 방식으로 평점 예측
• 어떤 특징?
  • 특정한 장르를 가진 영화 (예, 코미디, 액션, 드라마)에 대한 사용자 선호도
  • 사용자 요인 벡터 (예: 코미디(1), 액션(-3), 드라마(3))
  • 영화 장르 요소 (예: 코미디(1), 액션(3), 드라마(3)) $$ p_u^T = (1, -3, 3) $$ $$ q_i^T = (1, 3, 3) $$ $$ r_{ui} = q_i^Tp_u = 1 \cdot 1 - 3 \cdot 3 + 3 \cdot 3 = 1$$

• 사용자(행), 영화(열), 평점으로 구성된 R 행렬 - 사용자 특징을 추출할 수 있음

$$ R = \begin{bmatrix} \ -&\text{Alice}&-\\ \ -&\text{Bob}&-\\ \ -&\vdots&-\\ \ -&\text{Zoe}&-\\ \end{bmatrix} $$

\begin{align*} \text{Alice} &= 10\% \color{#048BA8}{\text{ Action fan}} + 10\% \color{#048BA8}{\text{ Comedy fan}} + 50\% \color{#048BA8}{\text{ Romance fan}} +\cdots\\ \text{Bob} &= 50\% \color{#048BA8}{\text{ Action fan}} + 30\% \color{#048BA8}{\text{ Comedy fan}} + 10\% \color{#048BA8}{\text{ Romance fan}} +\cdots\\ \text{Zoe} &= \cdots \end{align*}

• 영화(열), 사용자(행), 평점으로 구성된 transposed R 행렬 - 영화 특징을 추출할 수 있음

$$ R^T = \begin{bmatrix} \ -&\text{Titanic}&-\\ \ -&\text{Toy Story}&-\\ \ -&\vdots&-\\ \ -&\text{Fargo}&-\\ \end{bmatrix} $$

PCA는 차원을 축소하되, 전형적인 특징을 구하는 것¶

• 어떻게 하면 모든 점이 정보 손실 없이 투영될 수 있을까?
• 원래 공간에 퍼져 있는 정도를 변환된 공간에서 얼마나 잘 유지하느냐가 관건

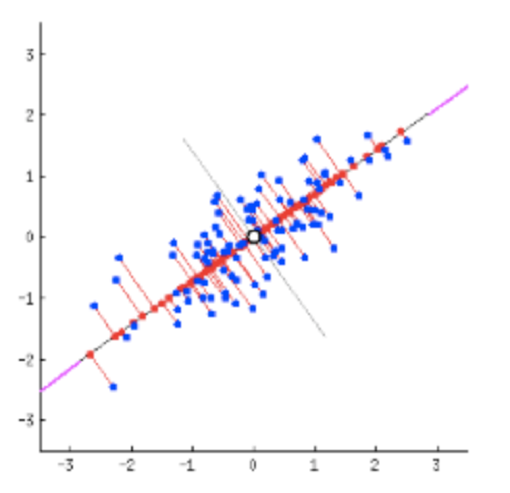
• PCA는 차원 축소를 공간에 정의된 어떤 축으로 투영해서 표현
• 이 때 어떤 축은 $D$ 차원의 단위 벡터 $u$로 표현 가능

• 축 $u$ 를 1차원 공간상의 정의할 때, 투영된 점은 $\hat{x}$ 으로 표기하고, PCA 신호를 $s = (s_1, s_2, ..., s_D)$ 로 표기하면, $$\hat{x} = u^T s$$ 이 되고,

• 이 문제는 $\hat{x}$ 의 분산을 가장 크게 하는 축(즉 단위 벡터 $u$)를 찾는 최적화 문제로 귀결된다.

• 우선 $\hat{x}$의 평균을 구해보자

$$\hat{x}_i, 1 \le i \le N의 평균, \bar{\hat{x}_i} = \dfrac{1}{N}\sum_{i=1}^N \hat{x}_i = \dfrac{1}{N}\sum_{i=1}^N u^T s_i = u^T(\dfrac{1}{N}\sum_{i=1}^N s_i) = u^T \bar{s}_i$$

• 다음으로 $\hat{x}$의 분산을 구해보자 $$\hat{x}_i, 1 \le i \le N의 분산, \hat{σ}^2 = \dfrac{1}{N}\sum_{i=1}^N (\hat{x}_i - \bar{\hat{x}})^2 = \dfrac{1}{N}\sum_{i=1}^N (u^T s_i - u^T \bar{s_i})^2$$

• 문제는 결국 $\hat{σ}^2$ 를 최대화하는 $u$를 찾는 것임

  • 위 식에서 $u$ 가 커지면 커질수록, $\hat{σ}^2$ 가 커짐?
• $u$ 는 단위 벡터이므로, $u^T u = 1$ 이 됨, 따라서 위 식은 조건부 최적화 문제로 바뀜
• 따라서 위 문제는 라그랑제 승수를 이용해서 다음과 같이 바꿔쓸 수 있음

$$L(u) = \dfrac{1}{N}\sum_{i=1}^N (u^T s_i - u^T \bar{s_i})^2 + \lambda(1 - u^T u)$$

• 즉, 전체 문제는 위 식의 값을 최대화하는 $u$를 찾는 문제로 바뀜

• 위 식을 $u$로 미분해봅니다.

$$\dfrac{L(u)}{\partial u} = \dfrac{\partial(\dfrac{1}{N}\sum_{i=1}^N (u^T s_i - u^T \bar{s_i})^2 + \lambda(1 - u^T u))}{\partial u}$$$$= \dfrac{2}{N}\sum_{i=1}^N (u^T s_i - u^T \bar{s_i})(s_i - \bar{s}) - 2\lambda u$$$$= 2u^T(\dfrac{1}{N}\sum_{i=1}^N (s_i - \bar{s})(s_i - \bar{s})^T) - 2\lambda u$$

• 여기서 $\dfrac{1}{N}\sum_{i=1}^N (s_i - \bar{s})(s_i - \bar{s})^T$ 는 공분산 행렬임, 따라서 이를 $\Sigma$ 로 바꾸자 $$= 2u^T\Sigma - 2\lambda u$$

• 여기서 $\Sigma$ 는 대칭이므로, $u^T\Sigma$ 를 $\Sigma u$로 바꿔쓸 수 있음 $$= 2\Sigma u - 2\lambda u$$

• $L(u)$ 를 최대화하는 $u$ 는 $\dfrac{\partial L(u)}{\partial u} = 0$을 만족하면 됨

• 따라서, 최종 식은 $$\Sigma u = \lambda u$$

• 여기에서 다음 정의를 확인해보자.

• 임의의 $n\times n$ 행렬 A에 대하여, 다음의 선형 시스템에서 0이 아닌 솔루션 벡터 K가 존재한다면 숫자 $\lambda$는 행렬 A의 고유값이다.$$AK=\lambda K$$ 이 때, 솔루션 벡터 K는 고유값 $\lambda$에 대응하는 고유 벡터 이다.

• $\Sigma$ 도 $n\times n$ 행렬이므로, $u$는 $\Sigma$ 의 고유 벡터(eigenvector), $\lambda$는 $\Sigma$ 의 고유값(eigenvalue)이 됨

• 변수(행)별로 평균을 0으로 centering한 행렬 X′를 만듬 (좌표계의 원점이 평균 벡터와 일치하도록 만듬)

• 공분산행렬은 다음 식으로 만들 수 있음

\begin{align*} \Sigma =cov(X)&=\frac { 1 }{ n-1 } X'{ X' }^{ T }\\\\ \end{align*}

• 공분산행렬을 기반으로 고유값과 고유벡터 구하기

• 고유값을 높은 순으로 정렬하고, 이에 대응하는 고유벡터와 순서를 맞춤

• 고유값

• 고유벡터

• 차원축소예 (고유값을 기준으로 가장 큰 d개의 고유 벡터 선택)

• 특징 벡터 추출